Comparison between 2D, 2.5D and 3D PTVs definition in treatment planning for conformal radiotherapy of organ-confined carcinoma of prostate
Yasser Assad Rashed, Ph. D. and Tounis El-sayed Ahmed M. D.
The Department of Clinical Oncology and Nuclear Medicine, Faculty of Medicine, Menuofia University.
Abstract:
Purpose: To evaluate the adequacy of planning target volume (PTV) coverage using a three-dimensional (3D) margin-growing method compared to a two-dimensional (2D) and two and-one-half-dimensional (2.5D) margin-growing methods in the conformal radiotherapy (CRT) planning of prostate cancer.
Patients and methods: PTV of 10 patients suffering from organ-confined prostate carcinoma was planned using ARTS 3D treatment planning system. The plan was performed by; 2D, 2.5D, and 3D techniques. The three PTVs were determined by expansion of the gross tumor volume (GTV) by a 1.0-cm margin. The former was obtained by automatically adding the margin in 2.5D and 3D for GTV. In 2D the former was obtained by manual contouring in CT slices. For each patient the three PTVs were compared to assess the deviations of the 2D and 2.5D PTVs from the 3D PTV. For all PTVs conformal plans were designed using the same number of fields for the three PTVs. For each patient dose-volume histograms (DVHs) and isodose distributions were calculated.
Results: The 2D and 2.5D margin-growing methods underestimated the PTV by 17.84 % (range 12.1-22) and by 19.62 % (range 13.7-23.2) respectively when compared to the 3D margin-growing method. The underdosage according to 2D, 2.5D, and 3D margins are 2.6 % (range 1-3.23), 2.11 % (range 0-4.30), and 1.29 % (range 1-2.11) respectively.
Conclusion: From the comparison between the DVHs and isodose distributions for different slices, the full 3D GTV-to-PTV expansion is recommended in CRT to avoid underdosage.
Keywords: PTV; Conformal radiotherapy; 2D; 2.5D; 3D; prostate carcinoma.
1. Introduction
Three-dimensional conformal radiotherapy (3D CRT) allows men with prostate cancer to be treated safely with high doses of radiation. Determination of the planning target volume (PTV) is an essential step in 3D CRT [1]. The precision of its delineation directly influences the quality of treatment [2-8]. Delineation of the prostate and seminal vesicles for CRT involves computed tomography (CT). Rectal and bladder contrast are helpful in defining these normal structures [9]. An urethrogram has been used to identify the inferior border of the prostate, which is often difficult on a transverse cut. Image-based beam’s eye view techniques have resulted in changes in 40% of the portal apertures, in comparison to conventional simulator methods of prostate target delineation [10]. The Gross tumor volume (GTV) is taken to be the prostate, seminal vesicles, and puboprostatic ligament.
The International Commission of Radiation Units and Measurements (ICRU) [11] has defined volumes for treatment planning that take into account the extent of the known gross tumor, the areas of likely microscopic extension, and daily variations in patient setup and tumor position. In prostate cancer, most authors believe that in general 0.5- to 1.0-cm is required to ensure coverage of extracapsular microscopic tumor extension [12-14]. Roach, et al. [12] suggested increasing the margin to 1.0-cm infero- laterally and 1.5-cm postero- laterally at the area of the neurovascular bundles where tumor extension through the capsule is prevalent. To generate the PTV, additional margin is added to account for patient setup variation and prostate movement secondary to rectal and bladder filling. The PTV should be designed so that it covers the clinical target volume (CTV) with high probability for every treatment [15].
There are many methods by which a predetermined margin can be added to the GTV [16-18]. A commonly used method has been to add a uniform margin to each transaxial GTV outline. However, this two-dimensional (2D) method can be inadequate in certain regions of a 3D target volume, as the margin is not added perpendicular to the GTV, therefore, it does not take into account the volumetric nature of the GTV [19, 20]. While most major centers practicing 3D conformal planning utilize 3D volume expansion methods. Many other centers utilize beams-eye-view (BEV) planning in CRT may still be use a laminar 2D margin method. Conformal 3D planning requires 3D spatial evaluation of the tumor borders in order to create the appropriate PTV [21].
This study compares the adequacy of PTV coverage resulting from the application of a uniform margin in 2.5D and 3D with the coverage provided by a conventional 2D margin in the conformal treatment of localized prostate cancer.
2. Material and Methods
2.1. Patients, tumors, and radiotherapy details
From October 2002 to March 2004, ten prostate cancer patients treated with CRT using a six-field technique with shaped beams in Menuofia University, Egypt were selected for this study. Six of the patients had stage T1 tumors and four had T2 tumors for which the seminal vesicles were part of the GTV. The median age was 62 years (range 51-74). The patients were simulated in supine position and submitted in the same position to a CT scan of the pelvis with a 0.2-cm step (thickness 0.2-cm) in the region of the prostate and the seminal vesicles and with a 0.5-cm step caudally down to the anus, and cranially up to the sigmoid colon (always including the top of the bladder).
2.2. The treatment planning system
The advanced radiation therapy treatment planning system (ARTS-3D TPS, version 2.2, March 2000) was used in this work. It is designed to run on high performance Unix graphics workstations. Advanced Visual System (AVS) enable the system to provide the most versatile 3D visualization and treatment planning features.
The 3D model for photon beam dose calculation allows for irregular beam shapes and the 3D geometry of the patient. Beam direction can be non-coplanar as defined through gantry, table and collimator rotations. Dose normalization and beam weighting are handled efficiently using a summation process to provide rapid evaluation of 2D and 3D dose distributions.
2.3. Analytical strategy
CT images of the clinical and added margin were transferred to the planning workstation. The GTV was outlined in all relevant slices. The GTV covers the prostate gland only (PO) and a GTV covers the prostate with the seminal vesicles (PSV). The position of the apex of the prostate was verified by use of sagittal reconstruction through the prostate. A margin of 1.0-cm was applied for each patient in these two groups PO and PSV to create the PTV. The margin for each GTV was created automatically using both 2.5D and 3D margin-growing algorithms and manually using 2D margin growing method.
2.4. PTV definitions
The 2D, 2.5D and 3D PTVs are available in ARTS-3D TPS. The 2.5D technique amounts rolling an ellipse with its major and minor axes defined by the specified margins along the border of the contour template to expand its boundary. This technique will result in ‘exact margins’ in the x–y plane, on a contour-by-contour basis. Margins as viewed on a volume basis will be uneven depending on the sloping of the volume surface.
The 3D technique uses an ellipsoid to roam along the surface of the volume template. This technique guarantees ‘exact margins’ on a volume basis, the margins on the x–y plane, by the technique, will be uneven. The 2D margin-growing method deals with each transaxial slice in succession. The difference between 2D and 2.5D is that the 2D method does not provide a margin superior and inferior to the GTV. To grow the 2D margin on GTV accurately, growing of the 2.5D is done and then the excess slice on the superior and inferior to the GTV is removed. In order to create an appropriate superior margin, the most superior GTV outline is copied onto the end of 2.5D margin. A similar process is used for the inferior region (Figure 1)
2.5. Treatment technique
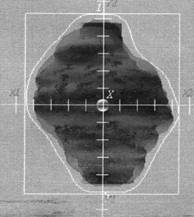
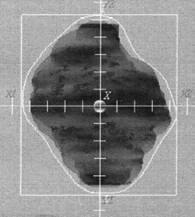
The importance of the choice of the irradiation technique in CRT of prostate cancer is related to the different doses, which can be delivered to the surrounding critical organs (rectum, bladder and femoral heads). There are many different techniques used in the CRT of the prostate cancer [22-29]. There is no technique better the other when considering all the organs at risk [29]. In this study, all patients were treated by six equally weighted fields (two lateral fields and four oblique fields at gantry angles 30º, 150º, 210º, and 330º) (Figure 2). The six-field arrangement conformed for three volumes; 2D, 2.5D, and 3D PTVs respectively. Figure 3 shows BEV of the conformed field at gantry angle 90º for the three PTVs. In figure 3a and 3b, the shape of the conformed field is almost the same except at the superior and inferior of PTV where the field was conformed to 2D and 2.5D PTVs respectively. But in Figure 3c the shape of the conformed field is wider than in figure 3a and 3b where the field was conformed to the 3D PTV.
2.6. Statistical evaluation
The significance of measured differences between different PTV-volumes of patients was tested with Student’s t-test for a confidence level of 0.05.
3. Results
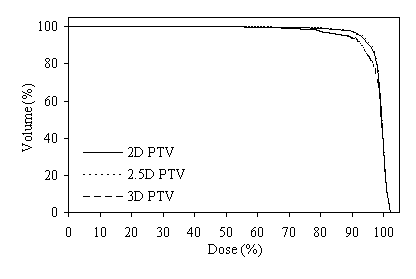
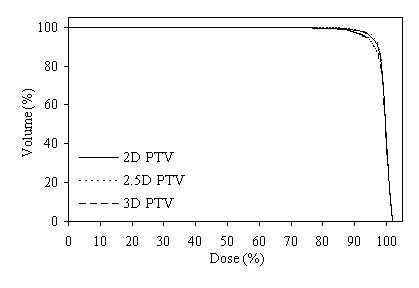
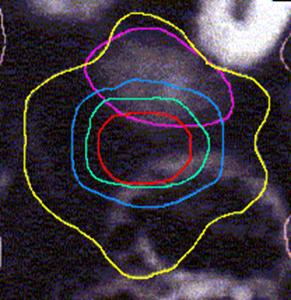
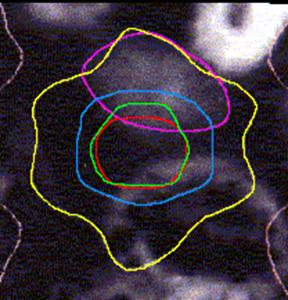
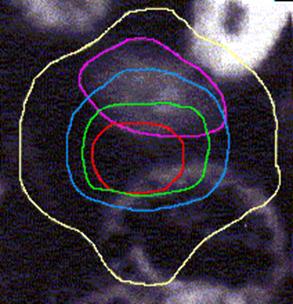
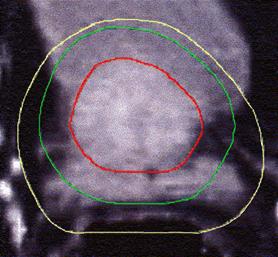
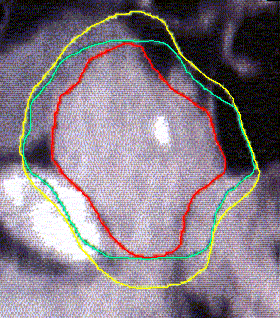
Figure 4 (a, b, and c) shows the axial position and sagittal and coronal reconstructions of the prostate in a plane near the superior part of the prostate for the same patient and the GTV (red line), 2D and 2.5D PTVs (green line) and 3D PTV (yellow line) are depicted. As expected, the 2D and 2.5D PTVs generally follows the GTV at exactly 1.0-cm in lateral and ventro-dorsal directions. Certain parts of the GTV responsible for a GTV-to-PTV extension as seen in the reconstruction may in themselves be invisible in that reconstruction. The 2D extension identify with the 2.5D extension except the regions after the end of the GTV in the cranio-caudal direction. These regions due to the slight variation in the volume of PTV between 2D and 2.5D extensions.
|
3D PTV |
|
+2.5D=2D PTV |
|
GTV |
|
GTV |
|
2.5D PTV |



Figure 1: The classification of the treatment volumes; GTV and three PTVs definitions. The GTV is the first degree of dark black, 2.5D is the second degree, and with adding the four corners to 2.5D give us the 2D. Finally the third degree of dark black (light black) is 3D PTV.

Figure 2: 6-field technique of two lateral fields and four oblique fields at gantry angles 30º, 150º, 210º, 330º.

A B C
Figure 3: BEV of the left lateral beam (gantry angle 90º) conformed to the three PTVs; (A) 2D PTV, (B) 2.5D PTV, and (C) 3D PTV. The conformal irradiation field (irregular white line) in A and B almost the same except at the superior and inferior of PTV. In C the conformal field is wider than in A and B.
Table 1 summarized the clinical patient prostate volumes generated by 2D, 2.5D, and 3D margin techniques for the clinical GTV. The mean volume of the GTV was 112.7 cc. The mean PTV defined by the 2D margin technique was 240.1 cm3 (range 171.4-309 cm3) and the mean PTV with 2.5D margin was 234.7 cm3 (range 169-300 cm3) while the mean PTV with the 3D margin was 292.9 cm3 (range 202.3-372 cm3). Overall, the PTVs generated with 3D algorithm were 12.1-22% larger than the PTVs generated by the 2D method and 13.7-23.2 larger than the PTVs generated by the 2.5D algorithm. The mean difference of the PTVs discrepancy between 2D and 3D is 17.8% and between 2.5D and 3D is 19.6%. The difference between the 2D and 2.5D PTVs is very highly significant (p<0.001) because slight variation in its volumes. While the difference between the 3D and both 2D and 2.5D PTVs is significant (p<0.05).
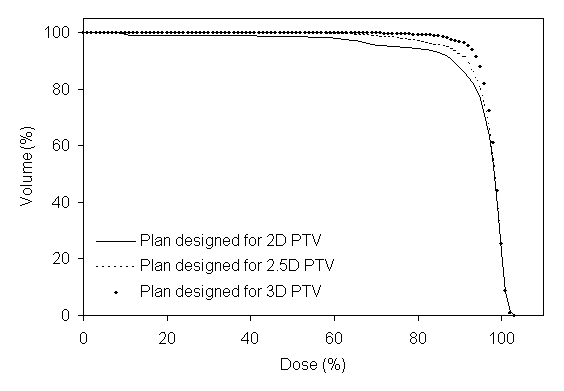
Figure 5 shows DVHs for the PTVs of prostate using the same six-field arrangement. In figure 5a the plan designed for the 2D PTV, in figure 5b the plan designed for the 2.5D PTV, and in figure 5c the plan designed for the 3D PTV. When the plan designed to the 2.5D PTV, the axial dimensions for the six field sizes are 10.4x8.9-, 10.4x9.7-, 10.4x9.9-, 10.4x9.6-, 10.4x8.9-, and 10.3x9.7-cm2 respectively started from the gantry angle 90º and rotated in clockwise direction.
|
2D & 2.5D |
![]()
![]()
![]()
|
3D PTV |

|
2D & 2.5D |

GTV |

![]()
|
3D PTV |


GTV |


Figure 4: GTV (red line), 2D and 2.5D PTVs (green line), and 3D (yellow line) show on the three positions; (A) Axial; (B) Sagittal; and (C) Coronal.